条件平差函数模型的QR分解解算

条件平差函数模型的 QR分解解算

王永 1，泥立丽 2

（ 1 山东科技大学资源学院，山东泰安， 271000； 2 泰山学院数学与统计学院，山东泰安， 271000）

摘 要：给出了条件平差函数模型的QR分解解算方法。对于条件平差函数模型，其系数矩阵的行数小于列数，传统上常利用经典最小二乘原理解算；多数情况下QR分解方法是针对行数大于列数且秩等于列数的矩阵进行的，因此本文结合这个实际，给出了条件平差函数模型的两种QR分解解算方法：直接计算方法和间接解算方法，并给出了推导公式。通过实例验证，这些方法得出的计算结果是一致的且有效的。

关键词：条件平差；间接平差；函数模型；QR分解；酉矩阵

基金：泰山学院人才基金项目（编号：Y-01-2017001）

The QR Decomposition Solution of the Conditional Adjustment Function Model

WANG Yong¹，NI Lili²

(1 College of Resources, Shandong University of Science and Technology, Tai 'an, 271000, Shandong,；2 School of Mathematics and Statistics, Tai 'an, 271000, Shandong)

Abstract: The method of solving QR decomposition of conditional adjustment function model is given. For the conditional adjustment function model, the number of rows in the coefficient matrix is less than the number of columns. In most cases, the QR decomposition method is used for the matrix with the number of rows greater than the number of columns and the rank equal to the number of columns. Therefore, this paper, combined with the actual situation, gives two QR decomposition solutions to the conditional adjustment function model: direct calculation method and indirect calculation method, and gives the derivation formula. The results obtained by these methods are consistent and effective.

Key words: Condition adjustment; Indirect adjustment; Function model; QR decomposition. The unitary matrix

0 引言

矩阵的QR分解在数值计算中扮演着重要的角色，是求解各类最小二乘问题和最优化问题的重要工具^[1]，为求解线性方程组提供了新的思路。QR分解目前大多应用于间接平差数学模型、秩亏自由网平差数学模型等的解算，对于条件平差的函数模型的解算应用相对较少。根据QR分解定理，所分解的矩阵要求是行数大于列数且列满秩，而对于条件平差的函数模型AV+W=0，其系数矩阵A为r行n列，行数小于列数。利用QR分解如何进行条件平差的解算呢？本文依据QR分解定理，推导了条件平差数学模型解算的公式，并从两个方面给出了相应的公式，并通过实例进行了验证。

1 理论部分

1.1 矩阵QR分解

定义：如果复（实）矩阵B可分解成一个酉（正交）矩阵Q和一个复（实）的上三角矩阵R的乘积，即B=QR，则称上式为矩阵B的一个QR分解。

定理：设方阵 非奇异，则存在酉（正交）矩阵Q和复（实）的正线（对角线全正数）上三角矩阵R，使得B=QR。证明见文献[4]。

推论：对于矩阵 且rankB=r，则B也可表示成一个n阶酉（正交）矩阵Q和r阶复（实）的正线上三角矩阵R的乘积，即 。证明见文献^[4]。

对于矩阵QR分解的方法包括Gram-Schmidt正交化法，Givens初等旋转矩阵法等，详情请参考文献[1]。

最小二乘广义逆：若B为方阵且非奇异，则其最小二乘广义逆为

；若B为长方阵，则其最小二乘广义逆为 。

1.2 条件平差模型的最小二乘解算

对于条件平差函数模型

（1）

式（1）中，r为多余观测数，n为总观测数，t为必要观测数且n=r＋t。利用最小二乘原理可得改正数 ，其中 为法方程系数矩阵。

1.3 条件平差模型的QR解算

1.3.1 直接计算方法

对于式（1），两边取转置并移项得

（2）

令 ，代入式（2）得

（3）

对式（3）两边右乘 ，从而可得 ，进一步转置可得

（4）

依据QR分解定理，得 ，取广义逆得

G＝ （5）

将式（5）两边取转置，得 ，代入式（4），得

（6）

式（6）即为条件方程的改正数V的QR分解直接解算公式。

1.3.2 间接计算方法

先将条件平差函数模型转化为间接平差函数模型，然后利用QR定理对间接平差函数模型的系数矩阵进行QR分解。

对于式（1），将系数矩阵A改为 ，改正数V改为 ，从而有

（7）

令 ， 为参数，且 中的t个改正数是相互独立的，对式（7）移项得

（8）

将式（8）左乘 ，则 ，令 ，并进行适当变换，则式（8）变为

（9）

令 ， ，综上可得误差方程式为

（10）

令 ， ，则式（10）变为

（11）

对式（11）中的系数矩阵B进行QR分解，并联合式（5）可得

（12）

联合式（11）和（12），进而求得观测值的改正数

（13）

式（13）即为条件方程的改正数V的QR分解间接解算公式。

2 算例及计算

2.1 算例

以文献^[3]中例5-3为例，如图1所示水准网为某高校学生实习时所布设的水准网，其中A为已知点，其高程H_A=10.121m，B、C、D为待定点，

图1 水准网

观测高差如下

h₁=﹢3.639 m，h₂ =﹢2.832m，h₃ =﹢2.726m，h₄ =﹢3.513m，h₅ =﹣6.353m；

设各观测高差为等精度观测，求各观测值的改正数。

由题意得n=5，t=3，r=2；矩阵形式的改正数条件方程为

其中系数矩阵 ，常数项 ；设权阵 （ 为单位对角矩阵）。

2.2 算例计算

2.2.1 利用经典最小二乘解算方法

将相关矩阵代入公式 ，得观测值的改正数为

；

2.2.2 利用直接解算方法

依据式（2）到（5），得相应矩阵如下：

依据 ，即则得矩阵Q和R分别如下

，

依据式（5）得B的广义逆G如下

最后可得观测值的改正数为

；

2.2.3 利用间接解算方法

由式（7）得相应矩阵如下

， ， ，

， ， ；

由式（10）和（11）得误差方程的系数矩阵B和常数项l如下

，

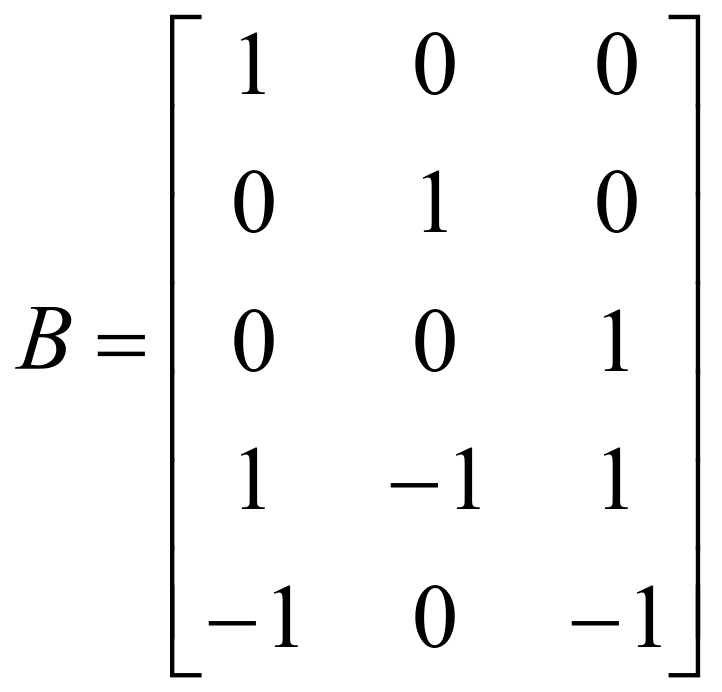对B进行QR分解，得Q、R矩阵分别如下

，

进而得B的广义逆矩阵G和参数 如下

，

由式（11）得改正数V如下

3 结论

对于以上算例，分别利用最小二乘原理、直接解算方法和间接解算方法得到的观测值的改正数V是一样的，说明了本文所推导的直接解算方法和间接解算方法的公式是正确的，填补了QR分解只针对于行数大于列数的矩阵分解问题。同时，直接解算方法更加简单、易于掌握；两种方法给出了一种利用QR方法进行线性方程组解算的思路。

但也要注意以下几点：

（1）本文计算时尽量保留了较多的小数位，是为了使最后的计算结果更精确；

（2）本文中计算过程中的各个矩阵是以表格的形式给出，显得更加直观。

参考文献

[1] 鲁铁定.总体最小二乘平差理论及其在测绘数据处理中的应用[D].武汉大学，2010年

[2] 姚吉利 等.条件平差与间接平差数学模型之间的相互转换[J].地矿测绘，2000（01）：25-26

[3] 泥立丽等.测量平差辅导及详解[M].化学工业出版社，2018年3月：65-66

[4] 王永 等.利用Excel绘制误差椭圆的方法[J].矿山测量，2008（05）：49-51+4

[5] 泥立丽 等.基于Excel的绘制误差曲线的方法[J].矿山测量，2010（03）：20-23+46+4

[6] 许章平 等.混沌理论支持下的桥梁变形监测研究[J].测绘通报，2019（06）：41-46

[7] 陈梦 等.基于分区回归模型确定建筑物倾斜状态[J].测绘通报，2019（03）：71-75

[8] 常增亮 等.电力工程变形监测数据处理系统设计与实现[J].测绘通报，2019（03）：71-75

[9] 辛明真 等.基于整体最小二乘的平面坐标转换模型比较[J].工程勘察，2015（05）：60-63+77

[10] 武汉大学测量平差学科组.误差理论与测量平差辅导（第3版）[M].武汉：武汉大学出版社，2017年8月

作者简介：

王永（1978-），男，汉族，山东新泰人，讲师，博士生，主要从事测量数据处理等方面的教学与科研工作。

6